整理常用的排序算法,主要包括:
- 选择排序
- 冒泡排序
- 归并排序
- 快速排序
- 插入排序
- 堆排序
策略以及时间开销
| 排序算法 | 基于的思想 | 时间开销 |
|---|---|---|
| 选择排序 | 蛮力法 | O(n^2) |
| 冒泡排序 | 蛮力法 | O(n^2) |
| 归并排序 | 分治法 | O(nlogn) |
| 快速排序 | 分治法 | O(nlogn) |
| 插入排序 | 减治法 | O(n^2) |
| 堆排序 | 减治法 | O(nlogn) |
部分排序的核心算法
归并排序
图解
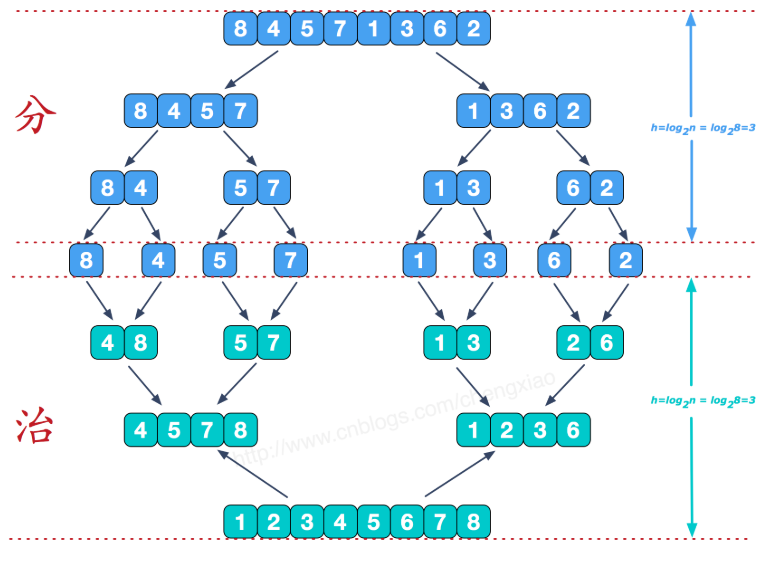
代码
/*
输入:待排序的数组r[n],待排序区间[s,t]
输出:升序序列r[s]~r[t]
1. 如果s==t,则待排序区间只有一个元素,返回
2. 计算划分重点:m=(s+t)/2
3. 对于前半个子序列以 r[s]~r[m]进行递归,继续划分
4. 对于后半个子序列以 r[m+1]~r[t]进行递归,继续划分
5. 合并划分后的子序列:
5.1 令i=s,j=m+1,k=s 在 i<=m&&j<=t时进行循环
5.1.1 按照升序依次在两个子序列选择元素放入r1[]临时数组,同时改变两个子序列的索引位置
6. 处理某个子序列未放完的元素
7. 将r1复制到r中
8. 待所有递归过程结束,打印r[]
*/
void MergeSort(int r[],int s,int t){
int m,r1[1000];
if(s==t) return; // 此时划分至只有一个元素了
else{
m = (s+t)/2; // 继续划分
MergeSort(r,s,m); // 划分前半个子序列
MergeSort(r,m+1,t); // 划分后半个子序列
Merge(r,r1,s,m,t); // 合并划分后的结果
for(int i=s;i<=t;i++){
r[i]=r1[i];
}
}
}
/* 合并函数 */
void Merge(int r[],int r1[],int s,int m,int t){
int i=s;
int j=m+1; // 分别标记原数组两个子序列的起始位置
int k=s; // 标记r1临时数组
while(i<=m&&j<=t){
if(r[i]<=r[j]) r1[k++]=r[i++];
else r1[k++]=r[j++];
}
// 进行收尾工作
while(i<=m) r1[k++]=r[i++];
while(j<=t) r1[k++]=r[j++];
}
快速排序
图解
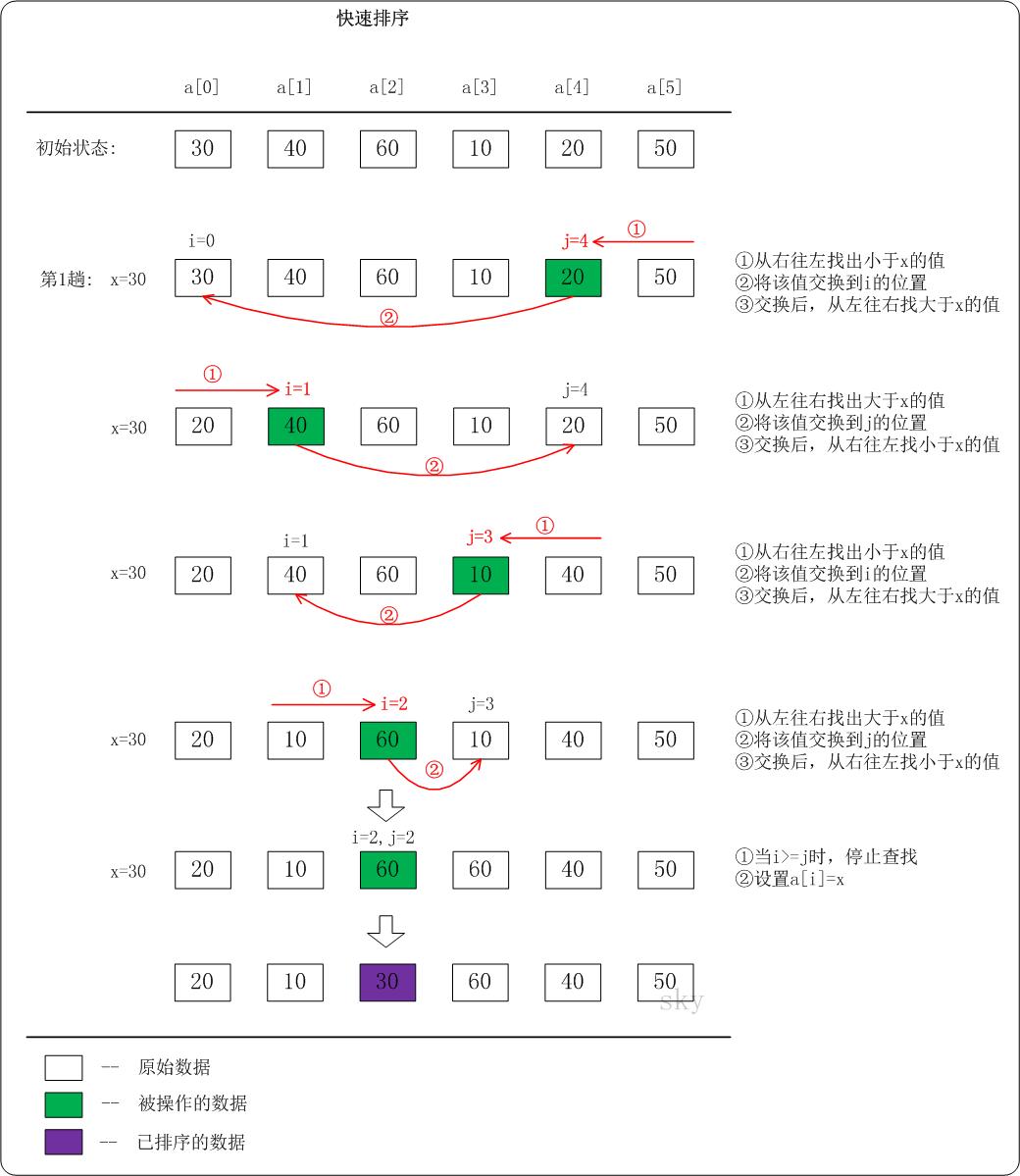
代码
/*
伪代码:
(假设以首元素为轴值)
输入:r[n],first,end
输出:升序排序的r[n]
1. 选定首元素即 r[first] 为轴值
2. 如果first<end
2.1 划分左右区间,获得轴值位置
2.1.1 令 i=first j=end, if i<j 做:
2.1.2 右侧扫描,if r[j]>轴值 j-- ;反之 swap(r[i],r[j])
2.1.3 左侧扫描,if r[i]<轴值 i++ ;反之 swap(r[i],r[j])
2.2 返回最后的i即为轴值的最新位置,pivot<-i
2.3 左孩子序列以:r,first,pivot-1 快排
2.4 右孩子序列以:r,pivot+1,end 快排
3. 最后输出排完序的r[n]
*/
void QuickSort(int r[],int first,int end){
int pivot; // 轴值
if(first<end){
pivot=Partition(r,first,end); // 划分子序列,pivot是轴值所在位置的索引
QuickSort(r,first,pivot-1); // 左子序列快排
QuickSort(r,pivot+1,end); // 右子序列快排
}
}
/* 划分子序列,求解轴值位置 */
int Partition(int r[],int first,int end){
int i=first;
int j=end;
while(i<j){
while(i<j&&r[i]<=r[j]) j--;
if(i<j){
int temp=r[i];
r[i]=r[j];
r[j]=temp;
i++;
}
while(i<j&&r[i]<=r[j]) i++;
if(i<j){
int temp=r[i];
r[i]=r[j];
r[j]=temp;
j--;
}
}
return i;
}
插入排序
图解

代码
// 设r[0]为哨兵,实际的数据从r[1]开始
for(int i=2;i<=n;i++){
r[0]=r[i]; // 使得r[0]一直为无序序列的第一个一个元素
for(int j=i-1;r[0]<r[j];j--){
r[j+1]=r[j]; // 如果待插入元素比有序序列中某个元素小,这个元素后移
}
r[j+1]=r[0];
}
堆排序
图解
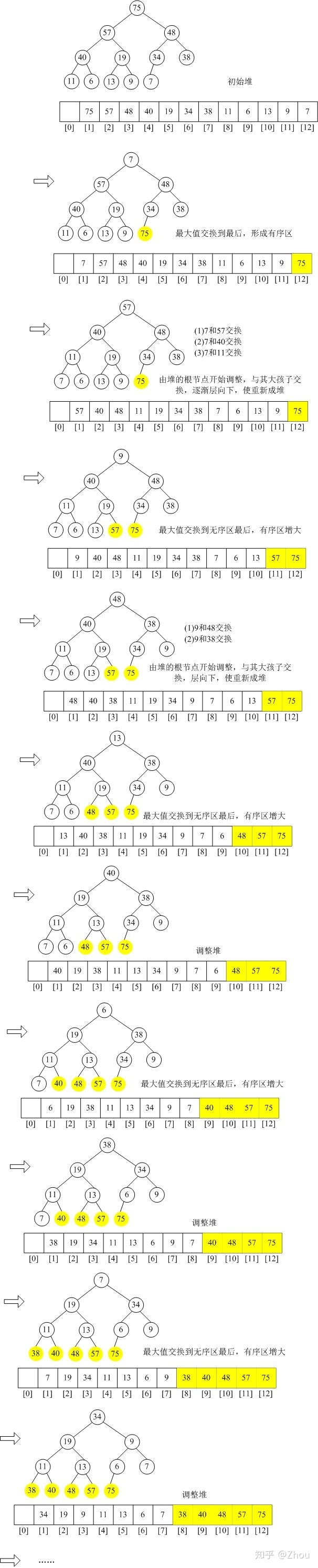
代码
/*
伪代码:
输入:r(k+1)~r(n)满足堆的条件,待筛选记录rk
输出:{r(k)',r(k+1)',...r(n)'}为大根堆
1. 设置i和j,分别指向要筛选的结点和其左孩子结点
2. 若ri已是叶子,则筛选完毕
否则,比较要筛选结点的左右孩子结点,并将j指向较大的结点
3. 将ri和rj进行比较,有以下两种情况:
3.1 如果ri>rj,则完全二叉树已是堆,筛选完毕
3.2 否则将ri和rj进行交换;令i=j,转步骤2继续执行
*/
void HeapSort(int r[],int n){
int i,temp;
for(i=(n-1)/2;i>=0;i--){ // 初始建堆,最后一个分支下标为(n-1)/2
SiftHeap(r,i,n);
}
for(i=1;i<=n-1;i++){
temp=r[0];
r[0]=r[n-i];
r[n-i]=temp;
SiftHeap(r,0,n-i); // 只需要调整根节点
}
}
void SiftHeap(int r[],int k,int n){
int i,j,temp; // 置i为要筛的结点,j为i的左孩子
i=k;
j=i*2+1;
while(j<n){
if(j<n-1&&r[j]<r[j+1]) j++; // 比较i的左右孩子,j为较大者
if(r[i]>r[j]) break;
else{
// 将被筛结点与结点j交换
temp=r[i];
r[i]=r[j];
r[j]=temp;
// 被筛节点位于原来结点j的位置
i=j;
j=2*i+1;
}
}
}