Simhash来自于Google Moses Charikar发表的一篇论文 “detecting near-duplicates for web crawling” 中提出了simhash算法,专门用来解决海量数据的去重任务。这个算法通过将一个文档转化为一个64位的二进制特征串,然后比较两个文档的特征串,如果这两个文档的特征串的海明距离小于某个值(一般来讲这个值为3),则说明这是相似文档。
Simhash原理
Simhash算法是局部敏感哈希的一种,其主要思想是将高维特征向量降维成低维的特征向量,通过比较两个向量的Hamming Distance来确定文章的相似度。所以Simhash算法就是通过比较两个Hamming Distance,以获取相似度,如果这个相似度小于某个规定的值,就说明这两个文本相似。
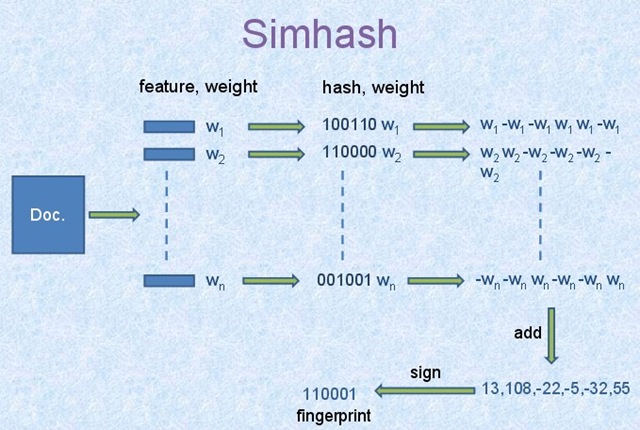
对于文本信息,我们需要对其作如下处理:
-
文本分词
首先我们需要对文本进行分词处理,也就是将文本的所包含的关键词提取出来,这部分我们可以使用目前常见的中文分词库来进行处理。这样我们就得到了一些关键词。
-
给关键词赋权
第二步需要根据权重给不同的关键词赋予权值。关于关键词的权重目前有很多种不同的计算方式,简单一些的比如根据关键词在文中出现的次数赋予权值,比较复杂但是更能体现实际意义的比如:TD-IDF算法、TextRank算法等等。目前所见的比较流行的分词工具都带有计算关键词权重的方法,所以在我们这个简单的实现中,这一步就用分词工具进行处理。这样我们获得了关键词以及其对应的权重。
-
对每个关键词进行hash运算
第三步我们对每个关键词进行hash运算,通常我们使用64位hash。这里我们为了方便用8位hash举例。 比如:
假设 “上海” 的hash值为:01011001
假设 “北京” 的hash值为:11001011
……
这样我们对每个关键词都得到了它们各自的hash。
-
对hash值加权处理
第四步加权处理所遵循的原则就是:如果某位是0,这位就变成 -Weight,反之这位就变成 Weight。
比如:
“上海” 的权值为:45.11
那么“上海”的特征向量就变为:-45.11 45.11 -45.11 45.11 45.11 -45.11 -45.11 45.11
“北京” 的权值为:32.09
那么“北京”的特征向量就变为:32.09 32.09 -32.09 -32.09 32.09 -32.09 32.09 32.09
……
-
对所用关键词的权值进行求和
第五步就是对所有关键字的特征向量的每一位的值分别求和,比如:
以两个关键词为例(“上海”、“北京”):-13.02 77.20 -77.20 13.02 77.20 -77.20 -13.02 77.20
-
转化为二进制
第六步,将最后的求和结果大于零位记录为1,小于零的记录为0,以上述为例:01011001
01011001就是这个文本的特征hash
-
计算hamming distance
我们假设两个文本的特征hash分别为:
00101110
00001111
它们的海明距离为2,我们就可以说这两个文章是相似的。
Golang代码实现
使用了一个Github的开源项目,里面的simhash是32位的,我们只是将其改成64位,只改动了一小点地方。
本次代码实现我们使用了几个开源项目:
第一个为golang实现的simhash的项目,一个为jieba分词库的golang版本。下面是代码:
package main
import (
"fmt"
"hash/fnv"
"simhash_similarity_jieba"
"strings"
)
type WordWeight struct {
Word string
Weight float64
}
func main() {
g := simhash.NewGoJieba()
srcStr := "已成为当前信息领域的一个新的研究热点 . 共识算法是区块链系统的关键要素之一 , 本文对目前已经提出的 32 种主流区块链共识算法进行了系统性的梳理与分析 . 需要说明的是 , 由于近年来共识算法研究发展较快 , 本文讨论的识算法可能仅为实际共识算法的一个子集 , 尚存在若干新兴或者小众的共识算法未加以讨论 , 同时一些较新的共识算法仍在不断试错和优化阶段 . 本文工作可望为后续的研究与应用提供有益的启发与借鉴 .以目前的研究现状而言区块链共识算法的未来研究趋势将主要侧重于区块链共识算法性评估、共识算法 – 激励机制的适配优化以及新型区块链结构下的共识创新三个方面 .首先 , 区块链共识算法在经历过一段百花齐放式的探索和创新之后 , 势必会趋向于收敛到新共识算法的性能评估和标准化方面的研究 . 目前 , 共识算法的评价指标各异 , 但一般均侧重于社会学角度的公平性和去中心化程度 , 经济学角度的能耗、成本与参与者的激励相容性以及计算机科学角度的可扩展性 ( 交易吞吐量、节点可扩展等 ) 、容错性和安全性等 . 如何结合具体需求和应用场景 自适应地实现针对特定性能评价目标的共识机制设计与算法优化 , 将是未来研究的热点之一 .其次 , 区块链的共识算法与激励机制是紧密耦合、不可分割的整体 , 同时二者互有侧重点 : 共识算法规定了矿工为维护区块链账本安全性、一致性和活性而必须遵守的行为规范和行动次序 ; 激励机制则规定了在共识过程中为鼓励矿工忠实、高效地验证区块链账本数据而发行的经济权益 , 通常包括代币发行机制、代币分配机制、交易费定价机制 [53] 等 .从研究角度来看 , 如果将区块链系统运作过程建模为矿工和矿池的大群体博弈过程 [54] 的话 , 那么共识算法将决定其博弈树的结构和形状、激励机制将决定矿工和矿池在博弈树中每个叶子结点的收益 . 因此 , 区块链共识算法和激励机制不仅各自存在独立优化的必要性 , 更为重要地是共识 – 激励二元耦合机制的联合优化、实现共识与激励的 “ 适配 ”, 这是解决区块链系统中不断涌现出的扣块攻击、自私挖矿等策略性行为、保障区块链系统健康稳定运行的关键问题 , 迫切需要未来研究的跟进 .最后 , 随着区块链技术的发展、特别是数据层的技术和底层拓扑结构的不断创新 , 目前已经涌现出若干新兴的区块 “ 链 ” 数据结构 , 例如有向无环图(Directed acyclic graph) 和哈希图 (HashGraph)等 . 这些新数据结构将以单一链条为基础的区块链技术的范畴展为基于图结构的区块 “ 链 ” 或分布式账本 . 例如适用于物联网支付场景的数字货币OTA 即采用称为 “Tangle ( 缠结 )” 的 DAG 拓扑结构 , 其共识过程以交易 ( 而非区块 ) 为粒度 , 每个交易都引证其他两个交易的合法性、形成 DAG 网络 ,因而可以实现无区块 (Blockless) 共识 ; HashGraph共识则更进一步 , 基于 Gossip of gossip 协议和虚拟投票等技术 , 以交易为粒度 , 在特定的 DAG 结构上2020自动实现公平和快速的拜占庭容错共识 . 这些新型区块"
dstStr := "那么共识算法将决定其博弈树的结构和形状、激励机制将决定矿工和矿池在博弈树中每个叶子结点的收益 . 因此 , 区块链共识算法和激励机制不仅各自存在独立优化的必要性 , 更为重要地是共识 – 激励二元耦合机制的联合优化、实现共识与激励的 “ 适配 ”, 这是解决区块链系统中不断涌现出的扣块攻击、自私挖矿等策略性行为、保障区块链系统健康稳定运行的关键问题 , 迫切需要未来研究的跟进 .最后 , 随着区块链技术的发展、特别是数据层的技术和底层拓扑结构的不断创新 , 目前已经涌现出若干新兴的区块 “ 链 ” 数据结构 , 例如有向无环图(Directed acyclic graph) 和哈希图 (HashGraph)等 . 这些新数据结构将以单一链条为基础的区块链技术的范畴展为基于图结构的区块 “ 链 ” 或分布式账本 . 例如适用于物联网支付场景的数字货币OTA 即采用称为 “Tangle ( 缠结 )” 的 DAG 拓扑结构 , 其共识过程以交易 ( 而非区块 ) 为粒度 , 每个交易都引证其他两个交易的合法性、形成 DAG 网络 ,因而可以实现无区块 (Blockless) 共识 ; HashGraph共识则更进一步 , 基于 Gossip of gossip 协议和虚拟投票等技术 , 以交易为粒度 , 在特定的 DAG 结构上2020自动实现公平和快速的拜占庭容错共识 . 这些新型区块拓扑结构及其共识算法是未来发展趋势之一 , 建立在这些新型数据结构之上的共识算法也值得深入研究"
// 第二个参数为分出关键词的个数
srcWordsWeight := g.C.ExtractWithWeight(srcStr, 22)
dstWordsWeight := g.C.ExtractWithWeight(dstStr, 11)
//fmt.Printf("srcWordsWeight: %v\n", srcWordsWeight)
//fmt.Printf("dstWordsWeight: %v\n", dstWordsWeight)
srcWords := make([]WordWeight, len(srcWordsWeight))
dstWords := make([]WordWeight, len(dstWordsWeight))
for i, ww := range srcWordsWeight {
word := WordWeight{Word: ww.Word, Weight: ww.Weight}
srcWords[i] = word
}
for i, ww := range dstWordsWeight {
word := WordWeight{Word: ww.Word, Weight: ww.Weight}
dstWords[i] = word
}
fmt.Printf("srcWords&weight:%v\n", srcWords)
fmt.Printf("dstWords&weight:%v\n", dstWords)
distance, err := SimHashSimilar64(srcWords, dstWords)
if err != nil {
fmt.Printf("failed: %v", err)
}
fmt.Printf("SimHashSimilar distance: %v", distance)
}
// 传入两个WordWeight类型的列表返回相似度值
func SimHashSimilar64(srcWordWeighs, dstWordWeights []WordWeight) (distance int, err error) {
srcFingerPrint, err := simhashFingerPrint64(srcWordWeighs)
if err != nil {
return
}
fmt.Println("srcFingerPrint: ", srcFingerPrint)
dstFingerPrint, err := simhashFingerPrint64(dstWordWeights)
if err != nil {
return
}
fmt.Println("dstFingerPrint: ", dstFingerPrint)
distance = hammingDistance(srcFingerPrint, dstFingerPrint)
return
}
// rewrite simhashFingerPrint
// 使用64位hash指纹进行运算
func simhashFingerPrint64(wordWeights []WordWeight) (fingerPrint []string, err error) {
// 使用64位创建64个元素的二进制权重
binaryWeights := make([]float64, 64)
for _, ww := range wordWeights {
bitHash := strHashBitCode64(ww.Word)
weights := calcWithWeight64(bitHash, ww.Weight) //binary每个元素与weight的乘积结果数组
binaryWeights, err = sliceInnerPlus64(binaryWeights, weights) //对每个hash数组求和
//fmt.Printf("ww.Word:%v, bitHash:%v, ww.Weight:%v, binaryWeights: %v\n", ww.Word,bitHash, ww.Weight, binaryWeights)
if err != nil {
return
}
}
fingerPrint = make([]string, 0)
// 将求和后的数组重新根据正负转化为2进制hash数组
for _, b := range binaryWeights {
if b > 0 { // bit 1
fingerPrint = append(fingerPrint, "1")
} else { // bit 0
fingerPrint = append(fingerPrint, "0")
}
}
return
}
// rewrite strHashBitCoin 64bit
// 返回一个64位的二进制字符串,也就是对这个关键字进行hash运算之后的hash字符串
func strHashBitCode64(str string) string {
h := fnv.New64a()
h.Write([]byte(str))
b := int64(h.Sum64())
return fmt.Sprintf("%064b", b)
}
// binary每个元素与weight的乘积结果数组,重写为64位操作
// 就是hash完关键字的64位二进制串上都变成 [ weight, -weight, -weight, ... ,weight]的形式
func calcWithWeight64(bitHash string, weight float64) []float64 {
// 首先分割字符串
bitHashs := strings.Split(bitHash, "")
// 构造一个长度为0的slice,之后往里添加元素
binarys := make([]float64, 0)
for _, bit := range bitHashs {
if bit == "0" {
// 根据simhash算法,如果这位上为0就乘以负的权值
binarys = append(binarys, float64(-1)*weight)
} else {
// 反正,这位为1就乘以正权值
binarys = append(binarys, float64(weight))
}
}
return binarys
}
// 对其每个求完权值并且进行完向量运算的64位hash特征串进行求和运算
// 假设arr2为第n个关键字,那么arr1就是前n-1个关键字每一位带权hash的和
func sliceInnerPlus64(arr1, arr2 [] float64) (dstArr []float64, err error) {
dstArr = make([]float64, len(arr1), len(arr1))
if arr1 == nil || arr2 == nil {
err = fmt.Errorf("sliceInnerPlus array nil")
return
}
if len(arr1) != len(arr2) {
err = fmt.Errorf("sliceInnerPlus array Length NOT match, %v != %v", len(arr1), len(arr2))
return
}
for i, v1 := range arr1 {
dstArr[i] = v1 + arr2[i]
}
return
}
func hammingDistance(arr1, arr2 []string) int {
count := 0
for i, v1 := range arr1 {
if v1 != arr2[i] {
count++
}
}
return count
}
具体函数细节请移步GitHub源码~
参考:
http://yanyiwu.com/work/2014/01/30/simhash-shi-xian-xiang-jie.html
https://wizardforcel.gitbooks.io/the-art-of-programming-by-july/content/06.03.html
关于更多的中文分词信息可以点击这里
关于Hamming Distance点击 -> 海明距离